linye's Blog

全端工程師心得分享

0%

[LeetCode]542. 01 Matrix

發表於 分類於 ，

Algorithm I 筆記撰寫計畫

敘述

這是 Algorithm I 的第九天第一個題目，總共有兩題。

  • 難度: Medium
  • 花費時間: 4 hr
  • 題目

給你一個 MxN binary matrix mat ，返回一個 MxN matrix 計算每個非零的值跟最近的零的距離，然後取代在他的值上。

上下左右才算相鄰，側面的就算要走兩格了。

點我開啟限制與範例

限制:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 104
  • 1 <= m * n <= 104
  • mat[i][j] is either 0 or 1.
  • There is at least one 0 in mat.

Example 1:

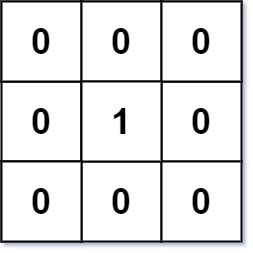
example-image-1

1
2
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

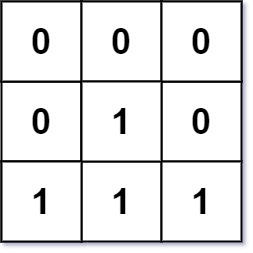
example-image-2

1
2
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]
點我開啟思路

思路

=下面的 iterative 方法宣告失敗

此方法最終會失敗是因為運算時間過久 time out

  1. 最大有可能有多少數字就運算幾次 (m + n -2)
  2. 遍歷矩陣
  3. 遇到 1 就進入 search 函式
  4. 重複做到完，就完成了

search 函式

  1. 找這個 node 的鄰居(上下左右)，全部塞進一個陣列裡
  2. 比較這個陣列，找出最小值 + 1 放回節點

matrix 會一直被迭代，越來越趨近於答案，如下範例

// 原 input
[[1,1,1]
,[1,1,1]
,[1,1,0]]

// iterated 1 time
[[2,2,2]
,[2,2,1]
,[2,1,0]]

// iterated 2 time
[[3,3,2]
,[3,2,1]
,[2,1,0]]

// iterated 3 time, completed
[[4,3,2]
,[3,2,1]
,[2,1,0]]

失敗的程式碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
function updateMatrix(mat: number[][]): number[][] {
  function update(row: number, col: number) {
    let neighborArr: number[] = [];
    // top
    if (mat[row - 1] && mat[row - 1][col] != undefined)
      neighborArr.push(mat[row - 1][col]);
    // right
    if (mat[row][col + 1] != undefined)
      neighborArr.push(mat[row][col + 1]);
    // button
    if (mat[row + 1] && mat[row + 1][col] != undefined)
      neighborArr.push(mat[row + 1][col]);
    // left
    if (mat[row][col - 1] != undefined)
      neighborArr.push(mat[row][col - 1]);

      console.log(...neighborArr)
    return (Math.min(...neighborArr) + 1);
  }

  for (let i = 0; i < mat.length + mat[0].length - 2; i++) {
    for (let row = 0; row < mat.length; row++) {
      for (let col = 0; col < mat[0].length; col++) {
        if (mat[row][col] === 0) continue;

        mat[row][col] = update(row, col);

      }
    }
  }

  return mat;
};

=下面的 bfs 方法宣告失敗

此方法最終會失敗是因為運算時間過久 time out

  1. 遍歷矩陣
  2. 遇到 0 跳過
  3. 遇到 1 進入 bfs 函式
  4. 全部走完回傳原矩陣

bfs 函式

  1. 從頭開始一圈一圈往外走
  2. 有遇到 0 就跳出函式
  3. 沒遇到 0 就繼續往外圈走

失敗的程式碼記錄

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
function updateMatrix(mat: number[][]): number[][] {

  // key is row, val is Array of col in this row.
  let visitedMap: Map<number, number[]>;

  // bfs search list
  let searchArr: number[][];

  function _search(row: number, col: number,
    pathCount: number = 0): number {
    // if this node is visited,or is edge of mat, than return now shartestPath.
    if ((visitedMap.get(row) && visitedMap.get(row)?.indexOf(col) != -1) ||
      row > mat.length - 1 || col > mat[0].length - 1 ||
      row < 0 || col < 0) return 0;

    //add this node into visitedMap.
    if (visitedMap.has(row)) {
      visitedMap.get(row)?.push(col);
    } else {
      visitedMap.set(row, [col]);
    }

    // if this node is 0 than return now pathCount
    if (mat[row][col] === 0) return pathCount;

    // if this node isn't 0, than move on next node (bfs).
    // push node into search list
    // top (row - 1)
    searchArr.push([row - 1, col, pathCount + 1]);
    // right (col + 1)
    searchArr.push([row, col + 1, pathCount + 1]);
    // button (row + 1)
    searchArr.push([row + 1, col, pathCount + 1]);
    // left (col - 1)
    searchArr.push([row, col - 1, pathCount + 1]);

    // bfs serarch
    while (searchArr.length > 0) {
      let shartestPath = _search(searchArr[0][0], searchArr[0][1], searchArr[0][2]);
      searchArr.shift();
      console.log('arr: ' + searchArr + " count: " + pathCount + " shortestPath: " + shartestPath);
      console.log(...visitedMap.values());
      console.log(...visitedMap.keys());

      if (shartestPath != 0) return shartestPath;
    }

    return 0;
  }

  for (let row = 0; row < mat.length; row++) {
    for (let col = 0; col < mat[0].length; col++) {
      if (mat[row][col] === 0) continue;

      if (mat[row][col] === 1) {
        // reset visitedMap
        visitedMap = new Map;
        searchArr = [];

        // do search
        console.log("this: " + row + " " + col)
        mat[row][col] = _search(row, col);
      }
    }
  }

  return mat;
};

=下面的 dfs 方法宣告失敗

  1. 遍歷矩陣
  2. 遇到 0 跳過
  3. 遇到 1 進入 bfs 函式
  4. 全部走完回傳原矩陣

dfs 函式

  1. 不能走走過的
  2. 只要最後有走到 0 的都比大小，取最小的
  3. 更新值

失敗的程式碼記錄

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
function updateMatrix(mat: number[][]): number[][] {

  // key is row, val is Array of col in this row.
  let visitedMap: Map<number, number[]>;

  /**
   * search the shortest path to the nearest 0 of this node (dfs)
   * @param row row num of this node
   * @param col col num of this node
   * @param PathCount counting the path num every call
   * @param shortestPath prep to compare, and return at the end
   * @returns shartestPath
   */
  function _search(row: number, col: number,
    PathCount: number = -1, shortestPath: number = mat.length + mat[0].length - 2): number {
    // console.log("row: " + row + " col: " + col);
    // console.log(...visitedMap.values());
    // console.log(...visitedMap.keys());

    // if this node is visited,or is edge of mat, than return now shartestPath.
    if ((visitedMap.get(row) && visitedMap.get(row)?.indexOf(col) != -1) ||
      row > mat.length - 1 || col > mat[0].length - 1 ||
      row < 0 || col < 0) return shortestPath;

    // Plus PathCount.
    PathCount++

    // if this node is 0, than return shortestPath.
    if (mat[row][col] === 0) {
      return Math.min(PathCount, shortestPath);
      visitedMap = new
    };

    //add this node into visitedMap.
    if (visitedMap.has(row)) {
      visitedMap.get(row)?.push(col);
    } else {
      visitedMap.set(row, [col]);
    }

    // if this node isn't 0, than move on next node (dfs).
    shortestPath = Math.min(shortestPath, _search(row + 1, col, PathCount, shortestPath));
    shortestPath = Math.min(shortestPath, _search(row - 1, col, PathCount, shortestPath));
    shortestPath = Math.min(shortestPath, _search(row, col + 1, PathCount, shortestPath));
    shortestPath = Math.min(shortestPath, _search(row, col - 1, PathCount, shortestPath));

    return shortestPath;
  }

  for (let row = 0; row < mat.length; row++) {
    for (let col = 0; col < mat[0].length; col++) {
      if (mat[row][col] === 0) continue;

      if (mat[row][col] === 1) {
        // reset visitedMap
        visitedMap = new Map;

        // do search
        mat[row][col] = _search(row, col);
      }
    }
  }

  return mat;
};

筆記

自己拚了 4 個小時，最後還是看解答才寫出來，但我有寫出比較相近的版本，請看上方思路裡的 iterative 版本。

這題有兩種做法:

第一種是使用 bfs ，但是對象是 0 ，我有想過這樣做，但是沒想到好的實現方法。

第二種是使用 DP 跟我寫的版本很類似，但他好在他不用迭代出答案，他只要正向遍歷一次，反向再遍歷一次即可。

解題步驟:

  • 正向遍歷一次 matrix
    • 遇到 0 跳過
    • 每個值都只拿自己左方及上方的值做比較，拿出最小的 + 1 放入 node.val = Math.min(top.val, left.val) + 1
  • 反向遍歷一次 matrix
    • 遇到 0 跳過
    • 每個值都與自己下方及右方的值做比較，拿出最小的 + 1 放入 node.val = Math.min(node.val, right.val, puttom.val) + 1

範例:

// input
[[0,1,1,1,1]
,[1,1,1,1,1]
,[1,1,0,1,1]]

// 先由左上往右下做檢查
[[0,1,2,2,2]
,[1,2,3,3,3]
,[2,3,0,1,2]]

// 再由右下往左上做檢查，答案就出來了
[[0,1,2,3,4]
,[1,2,1,2,3]
,[2,1,0,1,2]]

程式

function updateMatrix(mat: number[][]): number[][] {
  let longestPath = mat.length + mat[0].length - 2;

  // first, iterate by top left to buttom right
  for (let row = 0; row < mat.length; row++) {
    for (let col = 0; col < mat[0].length; col++) {
      if (mat[row][col] === 0) continue;

      // compare for the min val of this node's top and left.
      mat[row][col] = Math.min(
        mat[row - 1] ? mat[row - 1][col] + 1 : longestPath,// top
        mat[row][col - 1] != undefined ? mat[row][col - 1] + 1 : longestPath);// left
    }
  }

  // secend, iterate by buttom right to top left
  for (let row = mat.length - 1; row >= 0; row--) {
    for (let col = mat[0].length - 1; col >= 0; col--) {
      if (mat[row][col] === 0) continue;

      // compare for the min val of this node and it buttom and right.
      mat[row][col] = Math.min(
        mat[row][col],// this node
        mat[row + 1] ? mat[row + 1][col] + 1 : longestPath,// buttom
        mat[row][col + 1] != undefined ? mat[row][col + 1] + 1 : longestPath);// right
    }
  }

  return mat;
};

成績

score-image

參考資料