linye's Blog

全端工程師心得分享

0%

[LeetCode]1971. Find if Path Exists in Graph

發表於 分類於

給你一張包含 n 個節點的圖，這張圖的每個節點會沿著邊緣 edge 連向其他節點(不會連向自己)。
給你 source 跟 destination 兩個節點，判斷 source 有沒有辦法透過 dege 走到 destination 。

點我開啟限制與範例

限制:

  • 1 <= n <= 2 * 10^5
  • 0 <= edges.length <= 2 * 10^5
  • edges[i].length == 2
  • 0 <= ui, vi <= n - 1
  • ui != vi
  • 0 <= source, destination <= n - 1
  • There are no duplicate edges.
  • There are no self edges.

Example 1:

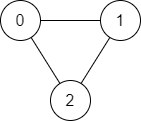
example-image-1

1
2
3
4
5
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

Example 2:

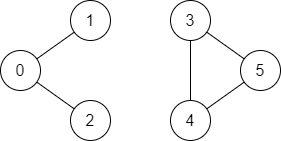
example-image-2

1
2
3
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

第一印象

  • 用遍歷做
  • 感覺用 BFS 會更好
  • 先確定 source 可以連到哪
  • 如果有碰到 destination 就回傳 true
  • 沒碰到，那就繼續往下個找。
  • 找過的 edge 刪掉
  • 最後沒有 edge 就回傳 false

筆記

  1. 深度優先遍歷陣列
  2. 找出最大跟最小的值
  3. 每次訪問都比大小，如果更大就更新結果
  4. 回傳結果

程式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function maxAncestorDiff(root: TreeNode | null): number {
    return _dfs(root!)
};

function _dfs(root: TreeNode, max = Number.MIN_VALUE, min = Number.MAX_VALUE, res: number = 0): number {
    if (root.val > max) max = root.val
    if (root.val < min) min = root.val

    res = Math.max(Math.abs(max - min), res)
    if (root.left) res = Math.max(_dfs(root.left, max, min, res))
    if (root.right) res = Math.max(_dfs(root.right, max, min, res))
    return res
}

成績

<!-- Language Runtime Beats Memory Usage Beats
TS iterative 91 ms 74.63% 44.7 MB 18.41%
TS recursive 80 ms 82.21% 43.9 MB 87.98% -->

score-image